Bacterial Growth Calculations

On this page you will learn how to carry out the following calculations related to bacterial growth:

• Calculating the area of a bacterial colony or a clear region on an agar gel plate.
• Calculating the number of bacteria in a population after a certain amount of time (when told the mean division time).

Calculating the area of a bacterial colony or clear region

In some experiments, we grow bacterial colonies on an agar gel plate and then work out the areas of those colonies.

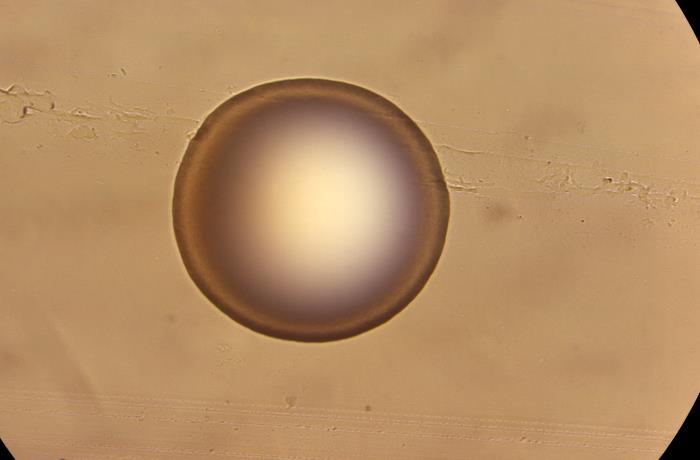
A bacterial colony growing on an agar gel plate.

In other experiments, we add antibiotics or disinfectants (two types of chemicals that kill bacteria) to an agar gel plate that has bacteria growing on it. Each antibiotic or disinfectant is added by taking a disc that is soaked in that chemical and placing it on the agar. This causes the bacteria to die around the disc, creating a clear region where there are no bacteria.

We then work out the area of that clear region.

Four antibiotic disks have been placed on an agar gel plate with bacteria growing on it. The bacteria have died around the discs, creating clear regions where there are no bacteria.

Regardless of whether we are measuring the area of a bacterial colony or the clear region around an antibiotic or disinfectant disc, what we are trying to do is find the area of a circle. Therefore, the method is the same.

First, we use a ruler to measure the diameter of the colony or clear region. The diameter is the greatest distance from one side to the other.

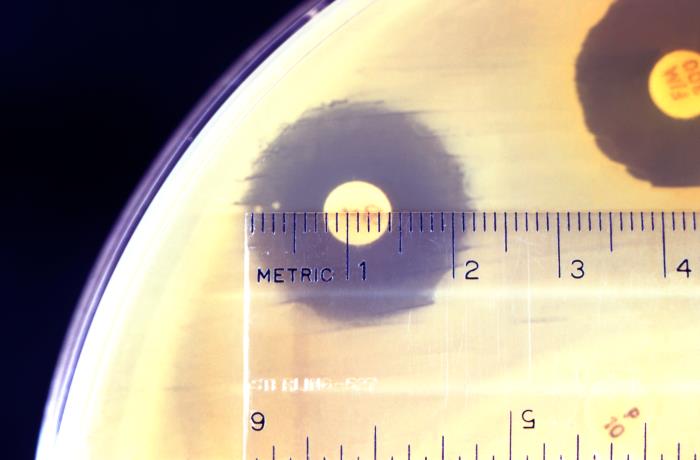
A scientist measuring the diameter of the clear region around an antibiotic disc.

In the image above, the diameter of the clear region is 2.2cm.

Next we need to find the radius of the colony or clear region. The radius is half of the diameter. Therefore, we divide the diameter that we measured by 2:

Radius = 2.2cm ÷ 2 = 1.1cm

So, in this case, the radius is 1.1cm.

The area of a circle can be calculated using the following formula:

Area of circle = π x radius²

This is often written as:

A = πr²

π is a number (approximately equal to 3.14) which you can access by pressing the π button on your calculator.

Since our bacterial colony or clear region is roughly circular, we can use this formula to calculate its area.

In our example, the radius is 1.1cm, so we calculate the area as follows:

Area = π x 1.1² = 3.801327111cm²

Rounding to three significant figures, we get 3.80cm². This is our answer.

Calculating the number of bacteria in a population after a certain amount of time

A single bacterium, through many rounds of cell division can give rise to a population of bacteria.

Bacteria dividing. Starting from a single bacterium, a population of bacteria is formed. Image: Stewart EJ, Madden R, Paul G, Taddei F (2005) via Wikimedia Commons (CC BY-SA 4.0 - https://creativecommons.org/licenses/by-sa/4.0/deed.en)

If you know the mean division time (that is, the average time it takes for the bacteria to complete one round of division), then you can work out how many bacteria there are in the population after a given amount of time.

For example, consider the following question:

A single bacterium, through many rounds of cell division, gives rise to a population of bacteria. The mean division time is 25 minutes. How many bacteria are in the population after 7 hours?

To answer this question, we need to calculate how many rounds of cell division have been completed.

We have been told that one round of cell division takes (on average) 25 minutes.

We have also been told that the bacteria have been dividing for 7 hours.

Since one of these pieces of information is in minutes and the other is in hours, we need to start by getting them into the same units. The easiest way to do this is to get them both into minutes.

To convert from hours to minutes, you multiply by 60 (since there are 60 minutes in an hour). So we multiply 7 by 60:

7 x 60 = 420

So we know that the bacteria have been dividing for 420 minutes.

We can now work out how many rounds of division have been completed. We do this by dividing the time they have been dividing for (420 minutes) by the mean division time (25 minutes):

420 ÷ 25 = 16.8

This means that the bacteria have completed 16 rounds of cell division and are 0.8 (that is, 80%) of the way through the next round. We want to know how many rounds of division have been fully completed, which is 16. In other words, we always drop anything after the decimal point.

Now that we know how many rounds of division have been completed, we can work out the number of bacteria.

To begin with there was one bacterium.

After the first round of division, this number doubled to give 2:

1 x 2 = 2

After the second round of division, this number doubled again to give four:

1 x 2 x 2 = 4

After the third round of division, this number doubled again to give eight:

1 x 2 x 2 x 2 = 8

We can see a pattern here. After each round of division, the number of bacteria is equal to 1 multiplied by 2 a certain number of times. The number of times that you multiply by 2 is equal to the number of divisions that have taken place (e.g. to calculate the number of bacteria after the third division, we multiplied by 2 three times).

Therefore, we can use this pattern to calculate the number of bacteria after any number of divisions, without having to go through the divisions one by one as we have been doing.

For example, after the seventh division, the number of bacteria would be equal to 1 multiplied by 2 seven times:

1 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128

The 1 at the beginning of this calculation doesn't actually do anything because multiplying by 1 doesn't do anything. Therefore, we don't need to write the 1.

So the number of bacteria after the seventh division is:

2 x 2 x 2 x 2 x 2 x 2 x 2 = 128

When we have a number being multiplied by itself repeatedly, we can write this using powers. So, rather than writing out seven 2s multiplied by each other we can just write the following:

2⁷ = 128

So we can see that the number of bacteria in the population after a certain number of divisions is simply equal to 2 to the power of the number of divisions:

Number of bacteria = 2^{Number of completed divisions}

In our question, we have worked out that 16 divisions have been completed. Therefore, the number of bacteria is:

2¹⁶ = 65,536

Rounding this to 3 significant figures we get:

65,500

We can also express this in standard form as:

6.55 x 10⁴

In doing this calculation we have assumed that none of the bacteria died during the 7 hours. This is an assumption we have to make in order to do the calculation.

Flashcards

Flashcards help you memorise information quickly. Copy each question onto its own flashcard and then write the answer on the other side. Testing yourself on these regularly will enable you to learn much more quickly than just reading and making notes.